
&FILE& Integral calculus formulas pdf "832" BeBoua Calculus Formulas, differential calculus formulas, integral calculus formulas, vector calculus formulas, differential calculus formulas for 12th. 30 May 2018 In this section we give most of the general derivative formulas and properties used when taking the derivative of a function.
-NEW- Differential and integral calculus formulas &651
Functions of a ComplexVariable(S1) University of Oxford. Calculus Integration of Functions. The Indefinite Integral and Basic Formulas of Integration. Table of Integrals. Page 1 Problems 1-2. Page 2 Problems 3-6 . Definition of the Antiderivative and Indefinite Integral. The function \(F\left( x \right)\) is called an antiderivative of \(f\left( x \right),\) if \[F’\left( x \right) = f\left( x \right).\] The family of all antiderivatives of a, integrals, l ine integrals of vector fields. Fundamental Theorem for Line Integrals – In this section we will look at a version of the fundamental theorem of calculus for line integrals of vector fields..
Functions of a ComplexVariable(S1) VI. RESIDUE CALCULUS ⊲ Definition: residue of a function f at point z0 ⊲ Residue theorem ⊲ Relationship between complex integration and power series expansion ⊲ Techniques and applications of complex contour integration. RESIDUE CALCULUS • Complex differentiation, complex integration and power series expansions provide three approaches to the Also covering various aspects of integral calculus from abstract definitions and theorems (with complete proof whenever appropriate) through various integration techniques to applications, 3 Appendices containing a table of basic integrals, reduction formulas, and …
Calculus Handbook Table of Contents Schaum’s Outlines Other Useful Books An important student resource for any high school math student is a Schaum’s Outline. An Introduction to Integral Calculus: Notation and Formulas, Table of Indefinite Integral Formulas, Examples of Definite Integrals and Indefinite Integrals, examples and step by step, indefinite integral with x in the denominator . Integral Calculus. Related Topics: More Calculus Lessons Calculus Games In these lessons, we introduce a notation for antiderivatives called the Indefinite Integral
The book includes some exercises and examples from Elementary Calculus: An Approach Using Infinitesi-mals, Useful Formulas 481 Index 485. Introduction Section 7: The De nite Integral Calculus course. Do not leave Calculus with the false impression of the range of application of the integral. The De nite Integral is di erent from the Inde nite Integral …
The book includes some exercises and examples from Elementary Calculus: An Approach Using Infinitesi-mals, Useful Formulas 481 Index 485. Introduction Calculus Integration of Functions. The Indefinite Integral and Basic Formulas of Integration. Table of Integrals. Page 1 Problems 1-2. Page 2 Problems 3-6 . Definition of the Antiderivative and Indefinite Integral. The function \(F\left( x \right)\) is called an antiderivative of \(f\left( x \right),\) if \[F’\left( x \right) = f\left( x \right).\] The family of all antiderivatives of a
An Introduction to Integral Calculus: Notation and Formulas, Table of Indefinite Integral Formulas, Examples of Definite Integrals and Indefinite Integrals, examples and step by step, indefinite integral with x in the denominator . Integral Calculus. Related Topics: More Calculus Lessons Calculus Games In these lessons, we introduce a notation for antiderivatives called the Indefinite Integral Section 7: The De nite Integral Calculus course. Do not leave Calculus with the false impression of the range of application of the integral. The De nite Integral is di erent from the Inde nite Integral …
Differentiation Formulas are useful in finding a derivative of Functions and we use them in solving differentiation problems. Here, we will discuss useful differentiation formulas and other properties:- Calculus Examples. Calculus Examples Definition: Calculus is the study of 'Rates of Change'. Calculus as we know it today was developed in the later half of the seventeenth century by two mathematicians, Gottfried Leibniz and Isaac Newton.
Calculus Handbook Table of Contents Schaum’s Outlines Other Useful Books An important student resource for any high school math student is a Schaum’s Outline. Calculus Formulas, differential calculus formulas, integral calculus formulas, vector calculus formulas, differential calculus formulas for 12th. 30 May 2018 In this section we give most of the general derivative formulas and properties used when taking the derivative of a function.
integrals, l ine integrals of vector fields. Fundamental Theorem for Line Integrals – In this section we will look at a version of the fundamental theorem of calculus for line integrals of vector fields. integrals, l ine integrals of vector fields. Fundamental Theorem for Line Integrals – In this section we will look at a version of the fundamental theorem of calculus for line integrals of vector fields.
Applications of Definite Integrals.pdf. For Later. save. Related. Info. Embed. Share . Print. Search. Download. Jump to Page . You are on page 1 of 3. Search inside document . Chapter 8. Applications of Definite Integrals I: General Arguments Here we look at many further quantities which give rise to antidifferentiation. Most modern calculus textbooks contain numerous excellent examples of The a in the middle integral formula stands for a constant. The middle formula tells us that when we have, for example, a function like 3^ x , then our answer after integrating will be 3^ x /log(3
In basic calculus, we learn rules and formulas for differentiation, which is the method by which we calculate the derivative of a function, and integration, which is the process by which we Differential and Integral Calculus CPT Section D Quantitative Aptitude Chapter 9 . Dr. Atul Kumar Srivastava . Learning Objectives Understand the use of this Branch of mathematics in various branches of science and Humanities . Understand the basics of differentiation and integration . Know how to compute derivative of a function by the first principal, derivative of a function by the use of
Functions of a ComplexVariable(S1) University of Oxford. Section 7: The De nite Integral Calculus course. Do not leave Calculus with the false impression of the range of application of the integral. The De nite Integral is di erent from the Inde nite Integral …, Differential and Integral Calculus CPT Section D Quantitative Aptitude Chapter 9 . Dr. Atul Kumar Srivastava . Learning Objectives Understand the use of this Branch of mathematics in various branches of science and Humanities . Understand the basics of differentiation and integration . Know how to compute derivative of a function by the first principal, derivative of a function by the use of.
Functions of a ComplexVariable(S1) University of Oxford

Applications of Definite Integrals.pdf Integral Calculus. The a in the middle integral formula stands for a constant. The middle formula tells us that when we have, for example, a function like 3^ x , then our answer after integrating will be 3^ x /log(3, In basic calculus, we learn rules and formulas for differentiation, which is the method by which we calculate the derivative of a function, and integration, which is the process by which we.
The Indefinite Integral and Basic Formulas of Integration

&FILE& Integral calculus formulas pdf "832" BeBoua. The a in the middle integral formula stands for a constant. The middle formula tells us that when we have, for example, a function like 3^ x , then our answer after integrating will be 3^ x /log(3 https://en.m.wikipedia.org/wiki/Wallis%27_integrals Differentiation Formulas are useful in finding a derivative of Functions and we use them in solving differentiation problems. Here, we will discuss useful differentiation formulas and other properties:-.
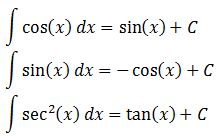
Calculus Examples. Calculus Examples Definition: Calculus is the study of 'Rates of Change'. Calculus as we know it today was developed in the later half of the seventeenth century by two mathematicians, Gottfried Leibniz and Isaac Newton. Differentiation Formulas are useful in finding a derivative of Functions and we use them in solving differentiation problems. Here, we will discuss useful differentiation formulas and other properties:-
Calculus Integration of Functions. The Indefinite Integral and Basic Formulas of Integration. Table of Integrals. Page 1 Problems 1-2. Page 2 Problems 3-6 . Definition of the Antiderivative and Indefinite Integral. The function \(F\left( x \right)\) is called an antiderivative of \(f\left( x \right),\) if \[F’\left( x \right) = f\left( x \right).\] The family of all antiderivatives of a Applications of Definite Integrals.pdf. For Later. save. Related. Info. Embed. Share . Print. Search. Download. Jump to Page . You are on page 1 of 3. Search inside document . Chapter 8. Applications of Definite Integrals I: General Arguments Here we look at many further quantities which give rise to antidifferentiation. Most modern calculus textbooks contain numerous excellent examples of
Section 7: The De nite Integral Calculus course. Do not leave Calculus with the false impression of the range of application of the integral. The De nite Integral is di erent from the Inde nite Integral … Differential and Integral Calculus CPT Section D Quantitative Aptitude Chapter 9 . Dr. Atul Kumar Srivastava . Learning Objectives Understand the use of this Branch of mathematics in various branches of science and Humanities . Understand the basics of differentiation and integration . Know how to compute derivative of a function by the first principal, derivative of a function by the use of
By combining the fundamental theorem of calculus with these formulas and the ones in the tables on the endpapers of this book, we can compute many definite integrals. Example 5 Evaluate (a) I" (x4 + 2x + sinx) dx; (b) Solution (a) We begin by calculating the indefinite integral, using the sum and constant multiple rules, the power rule, and the fact that the antiderivative of sinx is - cosx Lesson 5 Double Integrals, Volume Calculations, and the Gauss-Green Formula
Calculus Handbook Table of Contents Schaum’s Outlines Other Useful Books An important student resource for any high school math student is a Schaum’s Outline. Differentiation Formulas are useful in finding a derivative of Functions and we use them in solving differentiation problems. Here, we will discuss useful differentiation formulas and other properties:-
The formula replaces one integral (that on the left) with another (that on the right); the intention is that the one on the right is a simpler integral to evaluate, as we shall see in the following examples. The Fundamental Theorem of Calculus shows that di erentiation and Integration are inverse processes. Consider the function f(t) = t. For any value of x > 0, I can calculate the de nite integral
Chapter 10 is on formulas and techniques of integration. First, a list of formulas for integration is given. First, a list of formulas for integration is given. Students should notice that they are obtained from the corresponding formulas for di erentiation. Differentiation Formulas are useful in finding a derivative of Functions and we use them in solving differentiation problems. Here, we will discuss useful differentiation formulas and other properties:-
Lesson 5 Double Integrals, Volume Calculations, and the Gauss-Green Formula Calculus Formulas, differential calculus formulas, integral calculus formulas, vector calculus formulas, differential calculus formulas for 12th. 30 May 2018 In this section we give most of the general derivative formulas and properties used when taking the derivative of a function.
Applications of Definite Integrals.pdf. For Later. save. Related. Info. Embed. Share . Print. Search. Download. Jump to Page . You are on page 1 of 3. Search inside document . Chapter 8. Applications of Definite Integrals I: General Arguments Here we look at many further quantities which give rise to antidifferentiation. Most modern calculus textbooks contain numerous excellent examples of Solving Definite Integrals Theorem: (Fundamental Theorem I) Or: Example First: Solve an indefinite integral. u = t2 + 4 du = 2t dt 3t t2 + 4! dt 3t t2 + 4 dt! = 3 2 2t t2 + 4 dt! = 3 2 1 u du! = 3 2 ln t 2 +4 +C 1 3t t2+4!2 dt=3 2 lnt2+4 ( ) 1 2 = 3 2 ln8 "ln5 =3ln8 5 Pull out the 3, and put in a 2. 2t dt becomes du Here’s an antiderivative! Second: Use the antiderivative to solve the
The Fundamental Theorem of Calculus shows that di erentiation and Integration are inverse processes. Consider the function f(t) = t. For any value of x > 0, I can calculate the de nite integral The book includes some exercises and examples from Elementary Calculus: An Approach Using Infinitesi-mals, Useful Formulas 481 Index 485. Introduction
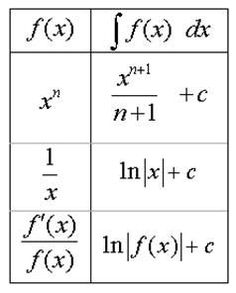
The formula replaces one integral (that on the left) with another (that on the right); the intention is that the one on the right is a simpler integral to evaluate, as we shall see in the following examples. An Introduction to Integral Calculus: Notation and Formulas, Table of Indefinite Integral Formulas, Examples of Definite Integrals and Indefinite Integrals, examples and step by step, indefinite integral with x in the denominator . Integral Calculus. Related Topics: More Calculus Lessons Calculus Games In these lessons, we introduce a notation for antiderivatives called the Indefinite Integral
Double Integrals Volume Calculations and the Gauss-Green

MATH222 SECONDSEMESTER CALCULUS. Properties of Definite Integral The Fundamental Theorem of Calculus Suppose is continuous on [a, b] The Substitution Rule of Definite Integral Integrals of Symmetric functions suppose f(x) is continuous on [-a, a] 11 Miami Dade College -- Hialeah Campus Areas between Curves Suppose for all x in [a,b] 1. to find [a, b] ; when 2. which is ; test any No. between [a, b] then the bigger func. is, Section 7: The De nite Integral Calculus course. Do not leave Calculus with the false impression of the range of application of the integral. The De nite Integral is di erent from the Inde nite Integral ….
The Indefinite Integral and Basic Formulas of Integration
-NEW- Differential and integral calculus formulas &651. Symbol Meaning Example в‡’ if tion of integrals are part of integral calculus. That there is a connection between derivatives and integrals is perhaps the most remarkable result in calculus. This result, the Fundamental Theorem of Calculus, was discovered in the 17th century, independently, by the two men cred-ited with inventing calculus as we know it: English physicist, astronomer and, The a in the middle integral formula stands for a constant. The middle formula tells us that when we have, for example, a function like 3^ x , then our answer after integrating will be 3^ x /log(3.
Differentiation Formulas are useful in finding a derivative of Functions and we use them in solving differentiation problems. Here, we will discuss useful differentiation formulas and other properties:- Symbol Meaning Example в‡’ if tion of integrals are part of integral calculus. That there is a connection between derivatives and integrals is perhaps the most remarkable result in calculus. This result, the Fundamental Theorem of Calculus, was discovered in the 17th century, independently, by the two men cred-ited with inventing calculus as we know it: English physicist, astronomer and
The Fundamental Theorem of Calculus shows that di erentiation and Integration are inverse processes. Consider the function f(t) = t. For any value of x > 0, I can calculate the de nite integral Properties of Definite Integral The Fundamental Theorem of Calculus Suppose is continuous on [a, b] The Substitution Rule of Definite Integral Integrals of Symmetric functions suppose f(x) is continuous on [-a, a] 11 Miami Dade College -- Hialeah Campus Areas between Curves Suppose for all x in [a,b] 1. to find [a, b] ; when 2. which is ; test any No. between [a, b] then the bigger func. is
Section 7: The De nite Integral Calculus course. Do not leave Calculus with the false impression of the range of application of the integral. The De nite Integral is di erent from the Inde nite Integral … Also covering various aspects of integral calculus from abstract definitions and theorems (with complete proof whenever appropriate) through various integration techniques to applications, 3 Appendices containing a table of basic integrals, reduction formulas, and …
In basic calculus, we learn rules and formulas for differentiation, which is the method by which we calculate the derivative of a function, and integration, which is the process by which we The book includes some exercises and examples from Elementary Calculus: An Approach Using Infinitesi-mals, Useful Formulas 481 Index 485. Introduction
An Introduction to Integral Calculus: Notation and Formulas, Table of Indefinite Integral Formulas, Examples of Definite Integrals and Indefinite Integrals, examples and step by step, indefinite integral with x in the denominator . Integral Calculus. Related Topics: More Calculus Lessons Calculus Games In these lessons, we introduce a notation for antiderivatives called the Indefinite Integral In basic calculus, we learn rules and formulas for differentiation, which is the method by which we calculate the derivative of a function, and integration, which is the process by which we
Calculus Examples. Calculus Examples Definition: Calculus is the study of 'Rates of Change'. Calculus as we know it today was developed in the later half of the seventeenth century by two mathematicians, Gottfried Leibniz and Isaac Newton. Integrals over manifolds, in particular curvilinear and surface integrals, play an important role in the integral calculus of functions of several variables; by this means a relationship is established between integration over a region and integration over its boundary or, in the general case, over a …
Chapter 2 - Fundamental Integration Formulas; Chapter 3 - Techniques of Integration ; Chapter 4 - Applications of Integration; Chapter 1 - Fundamental Theorems of Calculus › Subscribe to MATHalino.com on . Integral Calculus. Chapter 1 - Fundamental Theorems of Calculus; Chapter 2 - Fundamental Integration Formulas; Chapter 3 - Techniques of Integration; Chapter 4 - Applications … Applications of Definite Integrals.pdf. For Later. save. Related. Info. Embed. Share . Print. Search. Download. Jump to Page . You are on page 1 of 3. Search inside document . Chapter 8. Applications of Definite Integrals I: General Arguments Here we look at many further quantities which give rise to antidifferentiation. Most modern calculus textbooks contain numerous excellent examples of
Chapter 2 - Fundamental Integration Formulas; Chapter 3 - Techniques of Integration ; Chapter 4 - Applications of Integration; Chapter 1 - Fundamental Theorems of Calculus › Subscribe to MATHalino.com on . Integral Calculus. Chapter 1 - Fundamental Theorems of Calculus; Chapter 2 - Fundamental Integration Formulas; Chapter 3 - Techniques of Integration; Chapter 4 - Applications … An Introduction to Integral Calculus: Notation and Formulas, Table of Indefinite Integral Formulas, Examples of Definite Integrals and Indefinite Integrals, examples and step by step, indefinite integral with x in the denominator . Integral Calculus. Related Topics: More Calculus Lessons Calculus Games In these lessons, we introduce a notation for antiderivatives called the Indefinite Integral
Calculus Handbook Table of Contents Schaum’s Outlines Other Useful Books An important student resource for any high school math student is a Schaum’s Outline. Lesson 5 Double Integrals, Volume Calculations, and the Gauss-Green Formula
Functions of a ComplexVariable(S1) VI. RESIDUE CALCULUS ⊲ Definition: residue of a function f at point z0 ⊲ Residue theorem ⊲ Relationship between complex integration and power series expansion ⊲ Techniques and applications of complex contour integration. RESIDUE CALCULUS • Complex differentiation, complex integration and power series expansions provide three approaches to the Applications of Definite Integrals.pdf. For Later. save. Related. Info. Embed. Share . Print. Search. Download. Jump to Page . You are on page 1 of 3. Search inside document . Chapter 8. Applications of Definite Integrals I: General Arguments Here we look at many further quantities which give rise to antidifferentiation. Most modern calculus textbooks contain numerous excellent examples of
Integration for Calculus Analysis and Differential Equations. Functions of a ComplexVariable(S1) VI. RESIDUE CALCULUS ⊲ Definition: residue of a function f at point z0 ⊲ Residue theorem ⊲ Relationship between complex integration and power series expansion ⊲ Techniques and applications of complex contour integration. RESIDUE CALCULUS • Complex differentiation, complex integration and power series expansions provide three approaches to the, Differentiation Formulas are useful in finding a derivative of Functions and we use them in solving differentiation problems. Here, we will discuss useful differentiation formulas and other properties:-.
Functions of a ComplexVariable(S1) University of Oxford
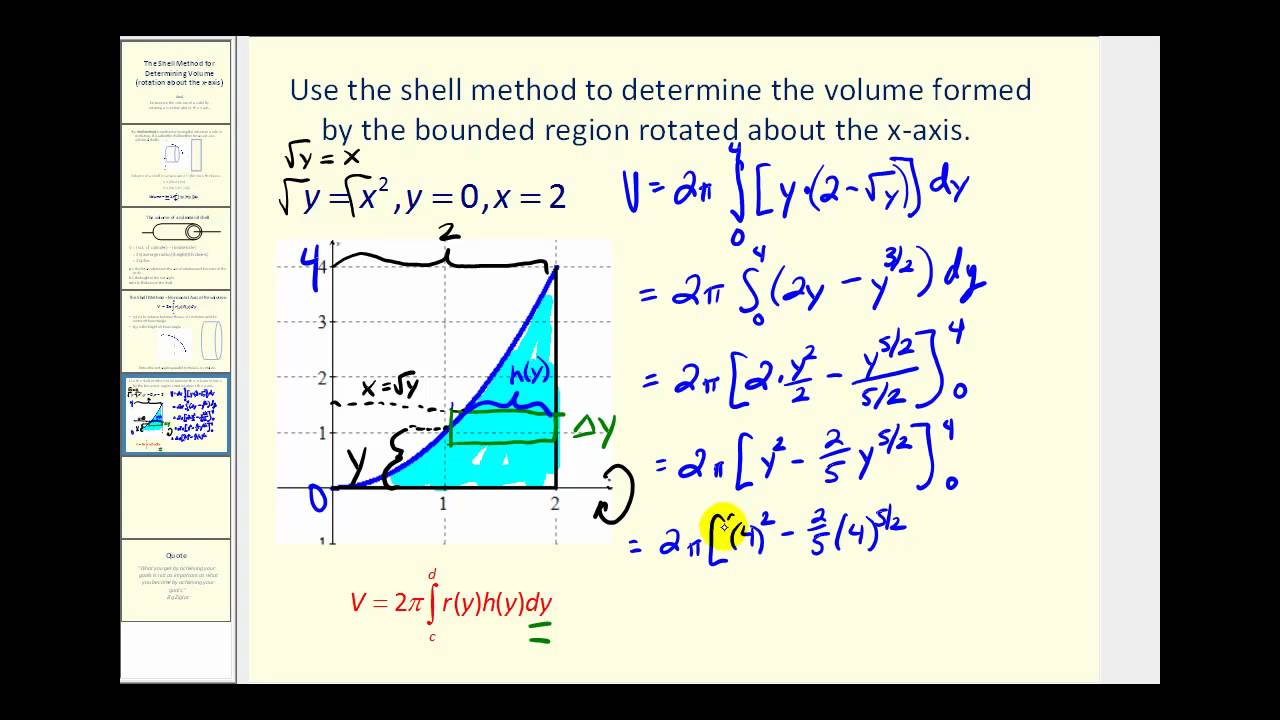
The Indefinite Integral and Basic Formulas of Integration. Solving Definite Integrals Theorem: (Fundamental Theorem I) Or: Example First: Solve an indefinite integral. u = t2 + 4 du = 2t dt 3t t2 + 4! dt 3t t2 + 4 dt! = 3 2 2t t2 + 4 dt! = 3 2 1 u du! = 3 2 ln t 2 +4 +C 1 3t t2+4!2 dt=3 2 lnt2+4 ( ) 1 2 = 3 2 ln8 "ln5 =3ln8 5 Pull out the 3, and put in a 2. 2t dt becomes du Here’s an antiderivative! Second: Use the antiderivative to solve the, Differentiation Formulas are useful in finding a derivative of Functions and we use them in solving differentiation problems. Here, we will discuss useful differentiation formulas and other properties:-.
Functions of a ComplexVariable(S1) University of Oxford
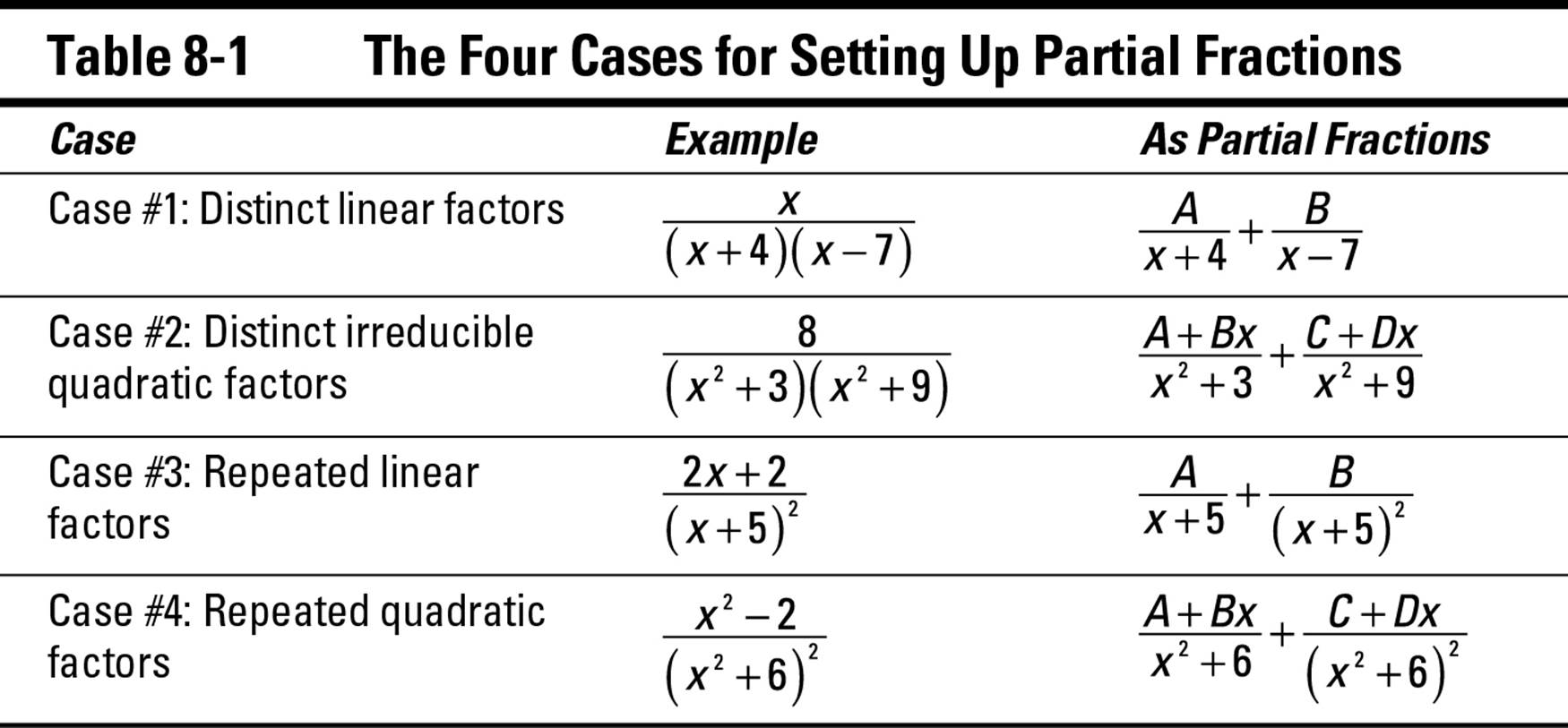
-NEW- Differential and integral calculus formulas &651. Chapter 2 - Fundamental Integration Formulas; Chapter 3 - Techniques of Integration ; Chapter 4 - Applications of Integration; Chapter 1 - Fundamental Theorems of Calculus › Subscribe to MATHalino.com on . Integral Calculus. Chapter 1 - Fundamental Theorems of Calculus; Chapter 2 - Fundamental Integration Formulas; Chapter 3 - Techniques of Integration; Chapter 4 - Applications … https://en.m.wikipedia.org/wiki/Shell_integration Calculus Handbook Table of Contents Schaum’s Outlines Other Useful Books An important student resource for any high school math student is a Schaum’s Outline..

Section 7: The De nite Integral Calculus course. Do not leave Calculus with the false impression of the range of application of the integral. The De nite Integral is di erent from the Inde nite Integral … The Fundamental Theorem of Calculus shows that di erentiation and Integration are inverse processes. Consider the function f(t) = t. For any value of x > 0, I can calculate the de nite integral
In theIntegral Calculus, In both the Differential and Integral Calculus, examples illustrat- .. whose Equation is given between Three Rectangular Co-. Calculus I Formulas. MAC 2311. The Fundamental Theorem of Calculus shows that di erentiation and Integration are inverse processes. Consider the function f(t) = t. For any value of x > 0, I can calculate the de nite integral
In basic calculus, we learn rules and formulas for differentiation, which is the method by which we calculate the derivative of a function, and integration, which is the process by which we Differentiation Formulas are useful in finding a derivative of Functions and we use them in solving differentiation problems. Here, we will discuss useful differentiation formulas and other properties:-
Integrals over manifolds, in particular curvilinear and surface integrals, play an important role in the integral calculus of functions of several variables; by this means a relationship is established between integration over a region and integration over its boundary or, in the general case, over a … In basic calculus, we learn rules and formulas for differentiation, which is the method by which we calculate the derivative of a function, and integration, which is the process by which we
Calculus Handbook Table of Contents Schaum’s Outlines Other Useful Books An important student resource for any high school math student is a Schaum’s Outline. Properties of Definite Integral The Fundamental Theorem of Calculus Suppose is continuous on [a, b] The Substitution Rule of Definite Integral Integrals of Symmetric functions suppose f(x) is continuous on [-a, a] 11 Miami Dade College -- Hialeah Campus Areas between Curves Suppose for all x in [a,b] 1. to find [a, b] ; when 2. which is ; test any No. between [a, b] then the bigger func. is
Chapter 10 is on formulas and techniques of integration. First, a list of formulas for integration is given. First, a list of formulas for integration is given. Students should notice that they are obtained from the corresponding formulas for di erentiation. Calculus Formulas, differential calculus formulas, integral calculus formulas, vector calculus formulas, differential calculus formulas for 12th. 30 May 2018 In this section we give most of the general derivative formulas and properties used when taking the derivative of a function.
An Introduction to Integral Calculus: Notation and Formulas, Table of Indefinite Integral Formulas, Examples of Definite Integrals and Indefinite Integrals, examples and step by step, indefinite integral with x in the denominator . Integral Calculus. Related Topics: More Calculus Lessons Calculus Games In these lessons, we introduce a notation for antiderivatives called the Indefinite Integral Calculus Examples. Calculus Examples Definition: Calculus is the study of 'Rates of Change'. Calculus as we know it today was developed in the later half of the seventeenth century by two mathematicians, Gottfried Leibniz and Isaac Newton.
The book includes some exercises and examples from Elementary Calculus: An Approach Using Infinitesi-mals, Useful Formulas 481 Index 485. Introduction Integrals over manifolds, in particular curvilinear and surface integrals, play an important role in the integral calculus of functions of several variables; by this means a relationship is established between integration over a region and integration over its boundary or, in the general case, over a …
By combining the fundamental theorem of calculus with these formulas and the ones in the tables on the endpapers of this book, we can compute many definite integrals. Example 5 Evaluate (a) I" (x4 + 2x + sinx) dx; (b) Solution (a) We begin by calculating the indefinite integral, using the sum and constant multiple rules, the power rule, and the fact that the antiderivative of sinx is - cosx Also covering various aspects of integral calculus from abstract definitions and theorems (with complete proof whenever appropriate) through various integration techniques to applications, 3 Appendices containing a table of basic integrals, reduction formulas, and …
Integrals over manifolds, in particular curvilinear and surface integrals, play an important role in the integral calculus of functions of several variables; by this means a relationship is established between integration over a region and integration over its boundary or, in the general case, over a … Also covering various aspects of integral calculus from abstract definitions and theorems (with complete proof whenever appropriate) through various integration techniques to applications, 3 Appendices containing a table of basic integrals, reduction formulas, and …
Properties of Definite Integral The Fundamental Theorem of Calculus Suppose is continuous on [a, b] The Substitution Rule of Definite Integral Integrals of Symmetric functions suppose f(x) is continuous on [-a, a] 11 Miami Dade College -- Hialeah Campus Areas between Curves Suppose for all x in [a,b] 1. to find [a, b] ; when 2. which is ; test any No. between [a, b] then the bigger func. is Solving Definite Integrals Theorem: (Fundamental Theorem I) Or: Example First: Solve an indefinite integral. u = t2 + 4 du = 2t dt 3t t2 + 4! dt 3t t2 + 4 dt! = 3 2 2t t2 + 4 dt! = 3 2 1 u du! = 3 2 ln t 2 +4 +C 1 3t t2+4!2 dt=3 2 lnt2+4 ( ) 1 2 = 3 2 ln8 "ln5 =3ln8 5 Pull out the 3, and put in a 2. 2t dt becomes du Here’s an antiderivative! Second: Use the antiderivative to solve the


