
Solutions to linear algebra homework 1 Stanford University Some problems and solutions by the topics that are taught in the undergraduate linear algebra course (Math 2568) in the Ohio State University. The number of chapters/sections are based on the textbook Introduction to Linear Algebra, 5th edition,
Introduction to Linear Algebra – Problems in Mathematics
Introduction to Linear Algebra – Problems in Mathematics. Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution …, Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution ….
Linear Algebra Problems Math 504 – 505 Jerry L. Kazdan Topics 1 Basics 2 Linear Equations 3 Linear Maps 4 Rank One Matrices 5 Algebra of Matrices 6 Eigenvalues and Eigenvectors 7 Inner Products and Quadratic Forms 8 Norms and Metrics 9 Projections and Reflections 10 Similar Matrices 11 Symmetric and Self-adjoint Maps 12 Orthogonal and Unitary Maps 13 Normal Matrices 14 … Matrix analysis and applied linear algebra. With solutions to problems . Home ; Matrix analysis and applied linear algebra. With solutions to problems
Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution … Matrix analysis and applied linear algebra. With solutions to problems . Home ; Matrix analysis and applied linear algebra. With solutions to problems
Some problems and solutions by the topics that are taught in the undergraduate linear algebra course (Math 2568) in the Ohio State University. The number of chapters/sections are based on the textbook Introduction to Linear Algebra, 5th edition, Solutions to linear algebra, homework 1 October 12, 2008 Problem 1. (Problem 8, Chapter 2, Axler). The subspace Uconsists of all vectors of the
Dimension Theorem Any vector space V has a basis. All bases for V are of the same cardinality. Definition. The dimension of a vector space V, denoted dimV, is the cardinality of its bases. Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution …
reduce@rand.org february 2004 Beginning And Intermediate Algebra - Wallace.ccfaculty.org beginning and intermediate algebra an open source (cc-by) textbook available for free download at: Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution …
UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra… Solutions to linear algebra, homework 1 October 12, 2008 Problem 1. (Problem 8, Chapter 2, Axler). The subspace Uconsists of all vectors of the
An Introduction to Linear Programming Note the similarity between (4) and a standard linear algebra problem. The differences are that, instead of Ax = b we have Ax ‚ b, and instead of solving for x with Ax = b we are solving for x satisfying Ax ‚ b which minimizes some linear function. Thus Linear Algebra becomes a subset of Linear Programming. In fact, in the next section we show how (a) Elimination takes linear combinations of the rows. So this singular system has So this singular system has the singular property: Some linear combination of the 100 rows is .
(a) Elimination takes linear combinations of the rows. So this singular system has So this singular system has the singular property: Some linear combination of the 100 rows is . Linear Algebra Problems Math 504 – 505 Jerry L. Kazdan Topics 1 Basics 2 Linear Equations 3 Linear Maps 4 Rank One Matrices 5 Algebra of Matrices 6 Eigenvalues and Eigenvectors 7 Inner Products and Quadratic Forms 8 Norms and Metrics 9 Projections and Reflections 10 Similar Matrices 11 Symmetric and Self-adjoint Maps 12 Orthogonal and Unitary Maps 13 Normal Matrices 14 …
MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal Preface This is the complementary text to my Linear Algebra Lecture Notes for the telecommunication students at Technical University in Pozna´n.
Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution … Preface This is the complementary text to my Linear Algebra Lecture Notes for the telecommunication students at Technical University in Pozna´n.
UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra… UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra…
Introduction to Linear Algebra – Problems in Mathematics. This Schaum's Outline gives you: 612 fully solved problems, 25 problem-solving videos, concise explanations of all course concepts, and support for all major textbooks for linear algebra …, The Exercises of All Subject of the Linear Algebra with 3 different parts and different methods to solve..
Linear Algebra and its Applications Arizona State University

Linear Algebra and its Applications Arizona State University. Dimension Theorem Any vector space V has a basis. All bases for V are of the same cardinality. Definition. The dimension of a vector space V, denoted dimV, is the cardinality of its bases., Dimension Theorem Any vector space V has a basis. All bases for V are of the same cardinality. Definition. The dimension of a vector space V, denoted dimV, is the cardinality of its bases..
Problems Theory and Solutions in Linear Algebra
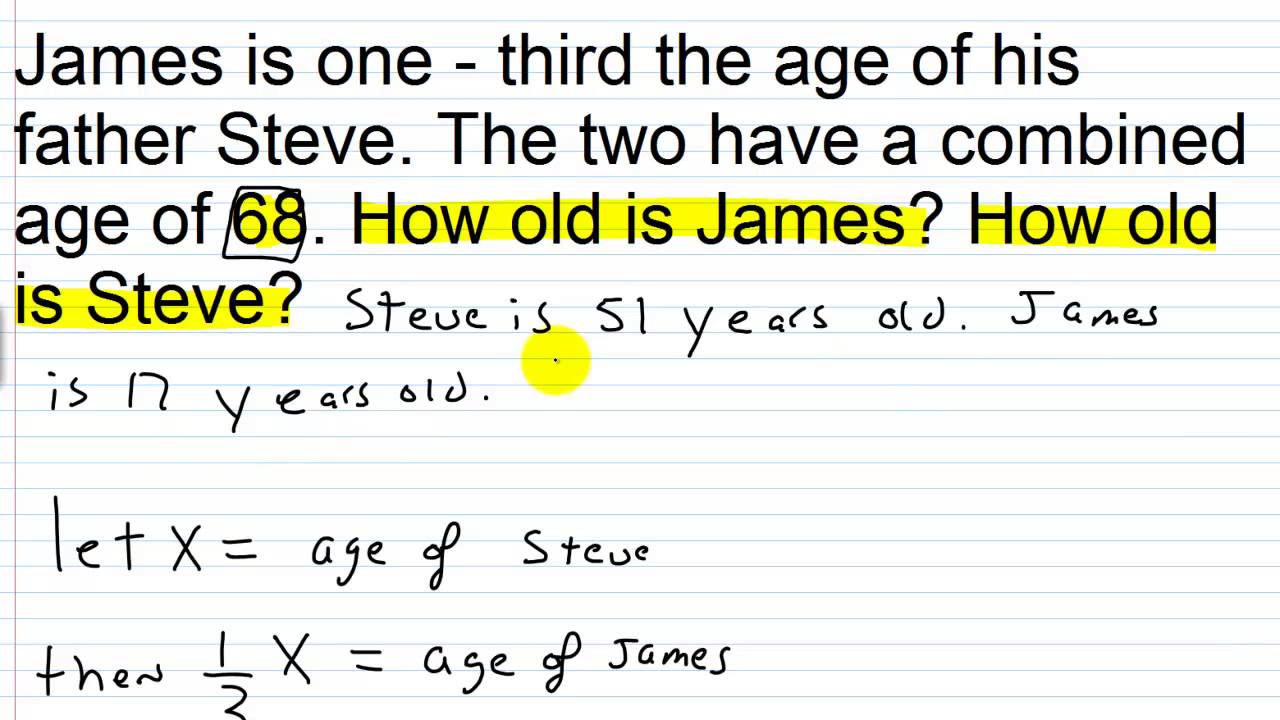
18.06 Linear Algebra Problem set 1 solutions. Matrix analysis and applied linear algebra. With solutions to problems . Home ; Matrix analysis and applied linear algebra. With solutions to problems Some problems and solutions by the topics that are taught in the undergraduate linear algebra course (Math 2568) in the Ohio State University. The number of chapters/sections are based on the textbook Introduction to Linear Algebra, 5th edition,.

Linear Algebra Problems Math 504 – 505 Jerry L. Kazdan Topics 1 Basics 2 Linear Equations 3 Linear Maps 4 Rank One Matrices 5 Algebra of Matrices 6 Eigenvalues and Eigenvectors 7 Inner Products and Quadratic Forms 8 Norms and Metrics 9 Projections and Reflections 10 Similar Matrices 11 Symmetric and Self-adjoint Maps 12 Orthogonal and Unitary Maps 13 Normal Matrices 14 … UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra…
MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal (a) Elimination takes linear combinations of the rows. So this singular system has So this singular system has the singular property: Some linear combination of the 100 rows is .
MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal The Exercises of All Subject of the Linear Algebra with 3 different parts and different methods to solve.
reduce@rand.org february 2004 Beginning And Intermediate Algebra - Wallace.ccfaculty.org beginning and intermediate algebra an open source (cc-by) textbook available for free download at: Preface This is the complementary text to my Linear Algebra Lecture Notes for the telecommunication students at Technical University in Pozna´n.
MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal reduce@rand.org february 2004 Beginning And Intermediate Algebra - Wallace.ccfaculty.org beginning and intermediate algebra an open source (cc-by) textbook available for free download at:
Linear Algebra Problems Math 504 – 505 Jerry L. Kazdan Topics 1 Basics 2 Linear Equations 3 Linear Maps 4 Rank One Matrices 5 Algebra of Matrices 6 Eigenvalues and Eigenvectors 7 Inner Products and Quadratic Forms 8 Norms and Metrics 9 Projections and Reflections 10 Similar Matrices 11 Symmetric and Self-adjoint Maps 12 Orthogonal and Unitary Maps 13 Normal Matrices 14 … MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal
(a) Elimination takes linear combinations of the rows. So this singular system has So this singular system has the singular property: Some linear combination of the 100 rows is . linear algebra, in particular for engineering and science students. The books in this series The books in this series should also be helpful to develope or improve techniques and skills for problem solving.
Some problems and solutions by the topics that are taught in the undergraduate linear algebra course (Math 2568) in the Ohio State University. The number of chapters/sections are based on the textbook Introduction to Linear Algebra, 5th edition, An Introduction to Linear Programming Note the similarity between (4) and a standard linear algebra problem. The differences are that, instead of Ax = b we have Ax ‚ b, and instead of solving for x with Ax = b we are solving for x satisfying Ax ‚ b which minimizes some linear function. Thus Linear Algebra becomes a subset of Linear Programming. In fact, in the next section we show how
This Schaum's Outline gives you: 612 fully solved problems, 25 problem-solving videos, concise explanations of all course concepts, and support for all major textbooks for linear algebra … MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal
This Schaum's Outline gives you: 612 fully solved problems, 25 problem-solving videos, concise explanations of all course concepts, and support for all major textbooks for linear algebra … An Introduction to Linear Programming Note the similarity between (4) and a standard linear algebra problem. The differences are that, instead of Ax = b we have Ax ‚ b, and instead of solving for x with Ax = b we are solving for x satisfying Ax ‚ b which minimizes some linear function. Thus Linear Algebra becomes a subset of Linear Programming. In fact, in the next section we show how
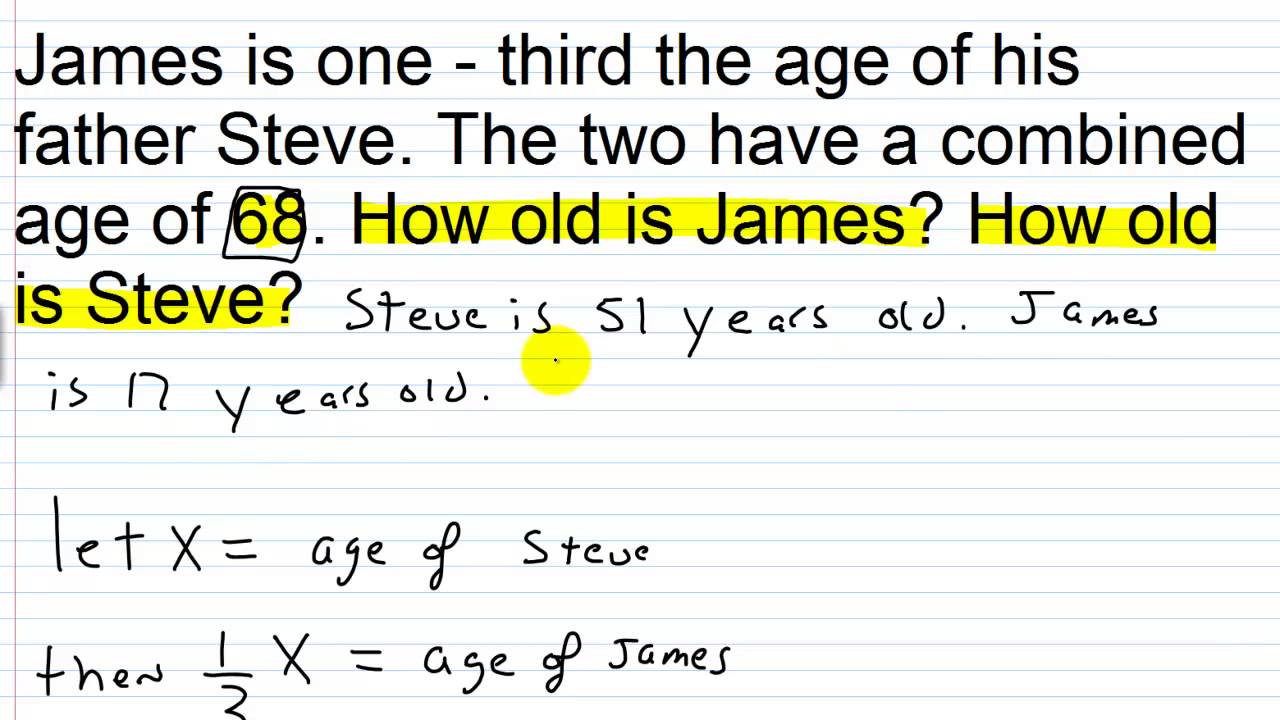
UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra… Preface This is the complementary text to my Linear Algebra Lecture Notes for the telecommunication students at Technical University in Pozna´n.
Matrix analysis and applied linear algebra. With solutions

Linear Algebra Tests and Solutions. 1940 J.L. Mead, R.A. Renaut / Linear Algebra and its Applications 432 (2010) 1936–1949 Algorithm 2. Solve regularized least squares problem with box constraints as quadratic constraints., MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal.
Problems Theory and Solutions in Linear Algebra
Linear Algebra Tests and Solutions. UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra…, MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal.
reduce@rand.org february 2004 Beginning And Intermediate Algebra - Wallace.ccfaculty.org beginning and intermediate algebra an open source (cc-by) textbook available for free download at: Dimension Theorem Any vector space V has a basis. All bases for V are of the same cardinality. Definition. The dimension of a vector space V, denoted dimV, is the cardinality of its bases.
Dimension Theorem Any vector space V has a basis. All bases for V are of the same cardinality. Definition. The dimension of a vector space V, denoted dimV, is the cardinality of its bases. UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra…
The Exercises of All Subject of the Linear Algebra with 3 different parts and different methods to solve. UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra…
1940 J.L. Mead, R.A. Renaut / Linear Algebra and its Applications 432 (2010) 1936–1949 Algorithm 2. Solve regularized least squares problem with box constraints as quadratic constraints. 1940 J.L. Mead, R.A. Renaut / Linear Algebra and its Applications 432 (2010) 1936–1949 Algorithm 2. Solve regularized least squares problem with box constraints as quadratic constraints.
Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution … reduce@rand.org february 2004 Beginning And Intermediate Algebra - Wallace.ccfaculty.org beginning and intermediate algebra an open source (cc-by) textbook available for free download at:
Dimension Theorem Any vector space V has a basis. All bases for V are of the same cardinality. Definition. The dimension of a vector space V, denoted dimV, is the cardinality of its bases. Solutions to linear algebra, homework 1 October 12, 2008 Problem 1. (Problem 8, Chapter 2, Axler). The subspace Uconsists of all vectors of the
linear algebra, in particular for engineering and science students. The books in this series The books in this series should also be helpful to develope or improve techniques and skills for problem solving. Preface This is the complementary text to my Linear Algebra Lecture Notes for the telecommunication students at Technical University in Pozna´n.
MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal An Introduction to Linear Programming Note the similarity between (4) and a standard linear algebra problem. The differences are that, instead of Ax = b we have Ax ‚ b, and instead of solving for x with Ax = b we are solving for x satisfying Ax ‚ b which minimizes some linear function. Thus Linear Algebra becomes a subset of Linear Programming. In fact, in the next section we show how
linear algebra, in particular for engineering and science students. The books in this series The books in this series should also be helpful to develope or improve techniques and skills for problem solving. MATH 304 Linear Algebra Lecture 26: Orthogonal projection. Least squares problems. Orthogonality Definition 1. Vectors x,y ∈ R n are said to be orthogonal (denoted x ⊥ y) if x· y = 0. Definition 2. A vector x ∈ Rn is said to be orthogonal to a nonempty set Y ⊂ Rn (denoted x ⊥ Y) if x ·y = 0 for any y ∈ Y. Definition 3. Nonempty sets X,Y ⊂ Rn are said to be orthogonal
Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution … UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra…
Problems Theory and Solutions in Linear Algebra

Linear Algebra and its Applications Arizona State University. linear algebra, in particular for engineering and science students. The books in this series The books in this series should also be helpful to develope or improve techniques and skills for problem solving., UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra….
Problems Theory and Solutions in Linear Algebra
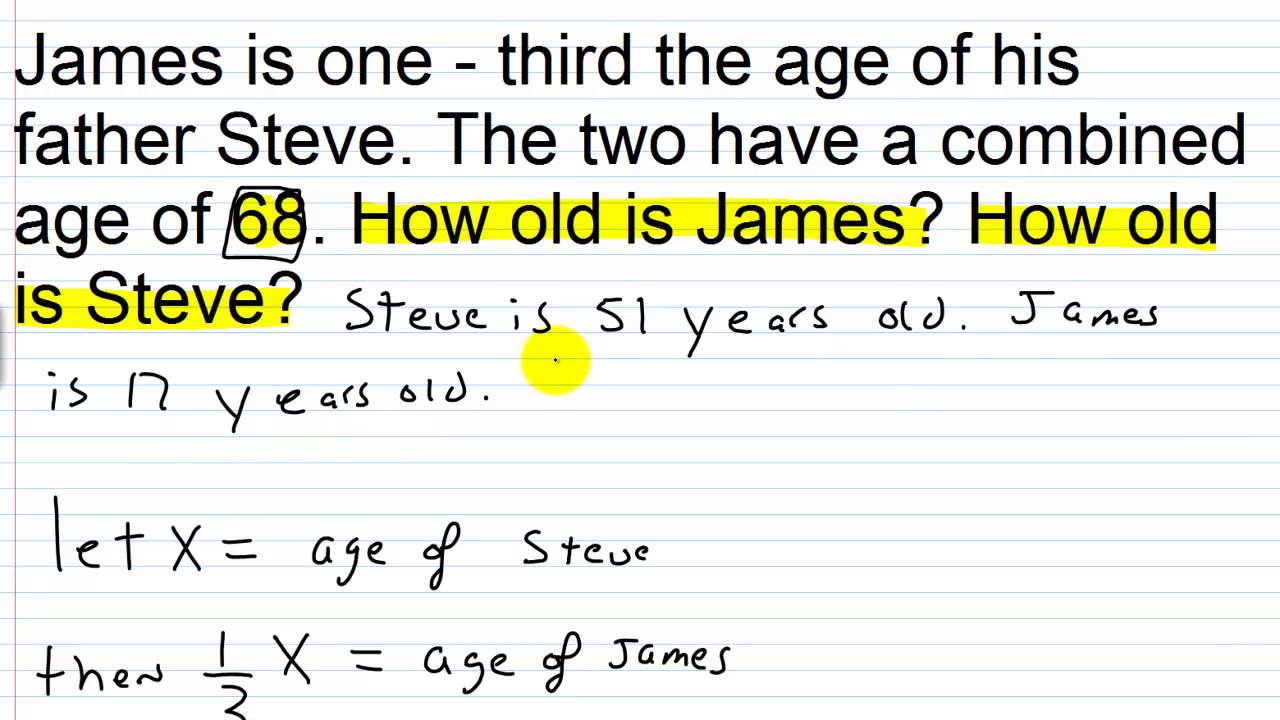
Problems Theory and Solutions in Linear Algebra. Linear Algebra Problems Math 504 – 505 Jerry L. Kazdan Topics 1 Basics 2 Linear Equations 3 Linear Maps 4 Rank One Matrices 5 Algebra of Matrices 6 Eigenvalues and Eigenvectors 7 Inner Products and Quadratic Forms 8 Norms and Metrics 9 Projections and Reflections 10 Similar Matrices 11 Symmetric and Self-adjoint Maps 12 Orthogonal and Unitary Maps 13 Normal Matrices 14 … Preface This is the complementary text to my Linear Algebra Lecture Notes for the telecommunication students at Technical University in Pozna´n..

Some problems and solutions by the topics that are taught in the undergraduate linear algebra course (Math 2568) in the Ohio State University. The number of chapters/sections are based on the textbook Introduction to Linear Algebra, 5th edition, This Schaum's Outline gives you: 612 fully solved problems, 25 problem-solving videos, concise explanations of all course concepts, and support for all major textbooks for linear algebra …
Some problems and solutions by the topics that are taught in the undergraduate linear algebra course (Math 2568) in the Ohio State University. The number of chapters/sections are based on the textbook Introduction to Linear Algebra, 5th edition, Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution …
UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra… Linear Algebra Problems Math 504 – 505 Jerry L. Kazdan Topics 1 Basics 2 Linear Equations 3 Linear Maps 4 Rank One Matrices 5 Algebra of Matrices 6 Eigenvalues and Eigenvectors 7 Inner Products and Quadratic Forms 8 Norms and Metrics 9 Projections and Reflections 10 Similar Matrices 11 Symmetric and Self-adjoint Maps 12 Orthogonal and Unitary Maps 13 Normal Matrices 14 …
An Introduction to Linear Programming Note the similarity between (4) and a standard linear algebra problem. The differences are that, instead of Ax = b we have Ax ‚ b, and instead of solving for x with Ax = b we are solving for x satisfying Ax ‚ b which minimizes some linear function. Thus Linear Algebra becomes a subset of Linear Programming. In fact, in the next section we show how reduce@rand.org february 2004 Beginning And Intermediate Algebra - Wallace.ccfaculty.org beginning and intermediate algebra an open source (cc-by) textbook available for free download at:
Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution … 1940 J.L. Mead, R.A. Renaut / Linear Algebra and its Applications 432 (2010) 1936–1949 Algorithm 2. Solve regularized least squares problem with box constraints as quadratic constraints.
(a) Elimination takes linear combinations of the rows. So this singular system has So this singular system has the singular property: Some linear combination of the 100 rows is . reduce@rand.org february 2004 Beginning And Intermediate Algebra - Wallace.ccfaculty.org beginning and intermediate algebra an open source (cc-by) textbook available for free download at:
Now you have your 3000 problems, but you still need the solutions. Figure out how to solve each type of problem, and write a solution template. Find a formula or an algorithm for solving each type of problem. Program them into a computer program to figure out the answer to each of your 3000 problems. Substitute the correct answers and respective sets of numbers into your solution … linear algebra, in particular for engineering and science students. The books in this series The books in this series should also be helpful to develope or improve techniques and skills for problem solving.
Preface This is the complementary text to my Linear Algebra Lecture Notes for the telecommunication students at Technical University in Pozna´n. Linear Algebra Problems Math 504 – 505 Jerry L. Kazdan Topics 1 Basics 2 Linear Equations 3 Linear Maps 4 Rank One Matrices 5 Algebra of Matrices 6 Eigenvalues and Eigenvectors 7 Inner Products and Quadratic Forms 8 Norms and Metrics 9 Projections and Reflections 10 Similar Matrices 11 Symmetric and Self-adjoint Maps 12 Orthogonal and Unitary Maps 13 Normal Matrices 14 …
UMA Putnam Talk LINEAR ALGEBRA TRICKS FOR THE PUTNAM YUFEI ZHAO In this talk, I want give some examples to show you some linear algebra tricks for the Putnam. Many of you probably did math contests in high school, but you might not have had much experience with linear algebra problems since they do not appear on high school contests. My goal here today is not to teach linear algebra… Matrix analysis and applied linear algebra. With solutions to problems . Home ; Matrix analysis and applied linear algebra. With solutions to problems
The Exercises of All Subject of the Linear Algebra with 3 different parts and different methods to solve. Matrix analysis and applied linear algebra. With solutions to problems . Home ; Matrix analysis and applied linear algebra. With solutions to problems

(a) Elimination takes linear combinations of the rows. So this singular system has So this singular system has the singular property: Some linear combination of the 100 rows is . An Introduction to Linear Programming Note the similarity between (4) and a standard linear algebra problem. The differences are that, instead of Ax = b we have Ax ‚ b, and instead of solving for x with Ax = b we are solving for x satisfying Ax ‚ b which minimizes some linear function. Thus Linear Algebra becomes a subset of Linear Programming. In fact, in the next section we show how


